La terza legge di Keplero

Osserva l'animazione qui a fianco. Ti mostra due pianeti in orbita attorno al Sole. L'orbita del pianeta bianco è più piccola di quella del pianeta verde. Cioè il pianeta bianco è più interno rispetto al pianeta verde. Con un righello potresti misurare che l'orbita esterna è circa una volta e mezza più grande di quella interna.

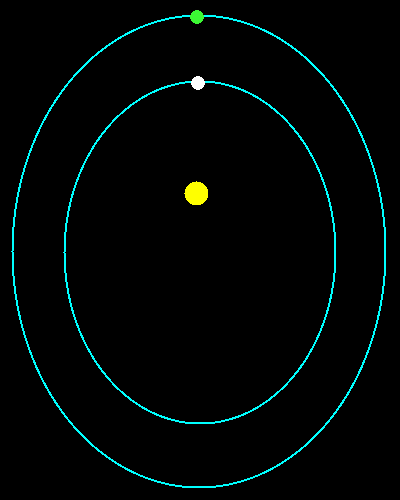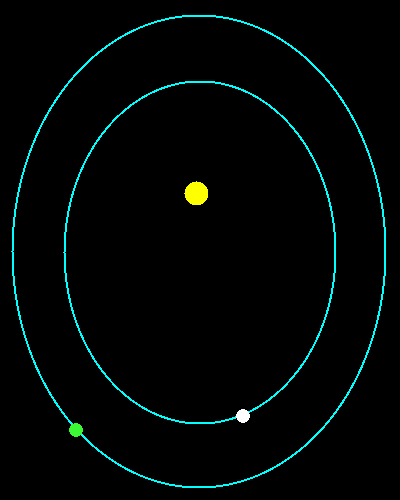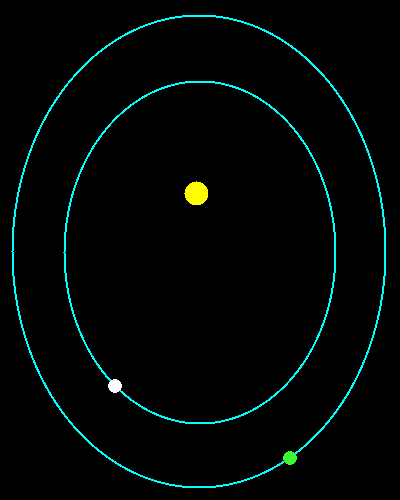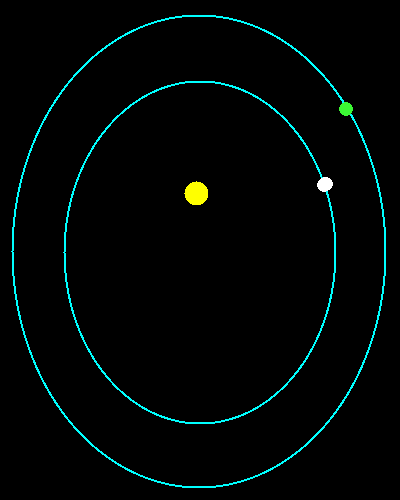
Precisamente le orbite sono disegnate in modo che la più grande è 1,5874... volte quella più piccola. Fra poco scoprirai perché questo numero misterioso!

Come previsto dalla prima legge i pianeti stanno su orbite ellittiche di cui il Sole occupa un fuoco. Inoltre entrambi i pianeti si muovono più velocemente quando la distanza dal Sole è minima, e più lentamente quando la distanza è massima. Essi rispettano quindi la seconda legge di Keplero.

Quale dei due pianeti si muove più velocemente? Evidentemente quello interno. In altri termini, il pianeta esterno impiega più tempo per percorrere la sua orbita. Il tempo necessario ad un pianeta per completare un'orbita viene detto periodo orbitale. Si può dunque dire che il periodo orbitale del pianeta esterno è maggiore del periodo orbitale del pianeta interno. La terza legge di Keplero prevede proprio questo. Via via che ci si allontana dal Sole i periodi orbitali diventano sempre più lunghi.

La regola è questa. Nel Sistema Solare i periodi orbitali elevati al quadrato sono proporzionali ai semiassi maggiori dell'orbita, elevati al cubo.

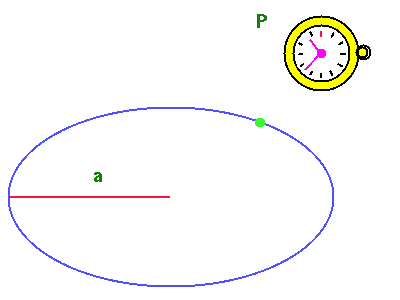
È possibile anche scrivere una formula. Chiama P il periodo orbitale e a il semiasse maggiore dell'orbita. In questa figura il semiasse maggiore è rappresentato in rosso. La regola si scrive allora

P² = k * a³

Il parametro k è un numero, uguale per tutti i pianeti. Fra un po' vedrai che non è importante sapere quant'è questo numero. Invece è importante notare che i periodi non dipendono dalla massa del pianeta, solo dalle dimensioni dell'orbita.

Questa regola vale non solo per il Sistema Solare, ma anche per tutti i sistemi composti da un corpo centrale con una massa molto maggiore di quella dei corpi che gli ruotano attorno.

La legge non ci dice qual è il valore di k. Supponi però di conoscere il periodo e la distanza dal Sole (o meglio il semiasse maggiore dell'orbita) di un qualsiasi pianeta. Allora sei in grado di calcolare il periodo orbitale di tutti gli altri pianeti in base alla loro distanza. Infatti dalla terza legge puoi anche scrivere

Guarda ad esempio i pianeti verde e bianco dell'animazione. La distanza del pianeta verde dal Sole è uguale alla distanza del pianeta bianco moltiplicata per circa 1,587. Qual è allora il rapporto tra i loro periodi? 1,587 elevato al cubo fa circa 4. Per la terza legge di Keplero questo è anche il rapporto dei periodi al quadrato. Il rapporto tra i periodi è allora la radice quadrata di 4, cioè 2. Quanto impiega il pianeta verde a percorrere la sua orbita? Il doppio del pianeta bianco! Mentre il pianeta verde compie un giro, il pianeta bianco ne ha già compiuti 2.

Ecco un filmato che illustra la terza legge di Keplero. Come nei primi, anche in questo l'audio è in inglese, ma prova ugualmente a vederlo.

(HEASARC), AVI, 2.6 Mb

Usando le 3 leggi di Keplero sei finalmente in grado di farti un'idea delle dimensioni del Sistema Solare dove vivi. Puoi disegnare una mappa dello spazio attorno al Sole, e usarla per pianificare le tue esplorazioni.

Vai avanti