La Parallasse

È facile trovare la distanza di un corpo se lo puoi raggiungere, ma prima degli anni '60 questo per la Luna non era possibile. Come fare allora? A dire il vero, un problema come questo si presenta spesso anche sulla Terra. Per esempio come si fa a misurare l'altezza di una montagna? Si può sfruttare il fatto che sulla Terra è possibile muoversi.

Guarda questa animazione. Immagina di essere al posto della persona, che si muove da destra a sinistra, e viceversa, davanti a due segni circolari disegnati sul terreno.

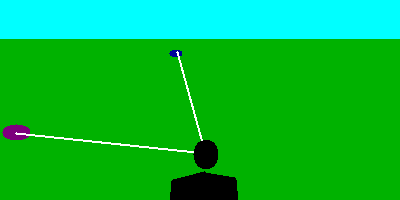
Vedresti quello che la figura ti mostra, cioè che il cerchio più vicino sembra muoversi di più rispetto al cerchio lontano.

Per vederlo meglio, guarda queste 2 figure. Ti mostrano la situazione quando la persona sta a destra delle figure e poi quando sta a sinistra.

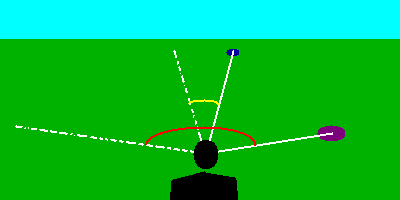
Le linee bianche sono le linee di vista dalla persona ai segnali. Nella seconda figura sono lasciate anche le linee di vista della prima figura.

Così puoi vedere che l'angolo compreso tra le linee di vista dirette al segnale più lontano (segnato in giallo) è più piccolo rispetto a quello relativo al segnale più vicino (segnato in rosso).

Per trovare la distanza di oggetti non raggiungibili puoi quindi sfruttare questa relazione tra il tuo spostamento lungo una retta e lo spostamento apparente di un oggetto.

Puoi fare come ti viene mostrato qui. Segui le indicazioni che ti vengono date cliccando sul pulsante >>. Il pallino nero rappresenta la tua posizione, quello viola l'oggetto lontano.

Se due triangoli sono simili, il rapporto tra la base e l'altezza nel primo triangolo è uguale al rapporto tra la base e l'altezza nel secondo triangolo. Avendo misurato i 3 angoli del triangolo grande puoi costruirti un triangolo piccolo, di cui puoi misurare sia la base sia l'altezza. Ad esempio potresti aver trovato che la base del triangolo grande è 6 m, che la base del triangolo piccolo è 12 cm e la sua altezza 30 cm. Allora il rapporto tra base e altezza per il triangolo piccolo è pari a 0,4 e lo stesso vale per il triangolo grande. L'altezza del triangolo grande è quindi 15 m. Questa corrisponde alla distanza tra la retta che hai segnato all'inizio e l'oggetto lontano.

Se il segnale lontano venisse ancor più allontanato l'angolo diventerebbe sempre più piccolo, sinché non riusciresti più ad apprezzare lo spostamento apparente. Questo accade infatti con la Luna. Essa è talmente lontana che la sua posizione apparente sembra fissa anche se ti muovi di parecchi chilometri. L'occhio umano riesce a distinguere solo gli spostamenti angolari più grandi di circa un primo (1'). Quest'angolo corrisponde ad una moneta da 500 lire vista da circa 90m di distanza. Affinché lo spostamento apparente della Luna sia di 1' devi muoverti di circa 112 chilometri!

Come si applica questo metodo alla Luna? Lo puoi scoprire qui.