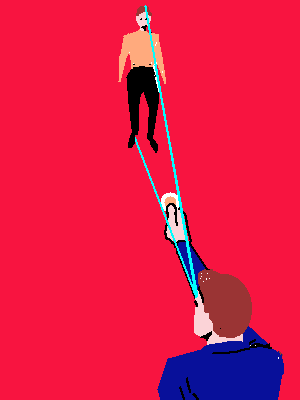LA LUNA

La Luna orbita attorno alla Terra. Hai visto in precedenza molte proprietà del suo moto. Ma che cos'è la Luna? Per averne un'idea devi determinare le sue caratteristiche fondamentali, dimensioni e massa.

Il primo passo in questa direzione è trovare la sua distanza.
È facile trovare la distanza di un corpo se lo puoi raggiungere, ma prima degli anni '60 questo per la Luna non era possibile. Come fare allora? A dire il vero, un problema come questo si presenta spesso anche sulla Terra. Per esempio come si fa a misurare l'altezza di una montagna? Si può sfruttare il fatto che sulla Terra è possibile muoversi.

Guarda questa animazione. Immagina di essere al posto della persona, che si muove da destra a sinistra, e viceversa, davanti a due segni circolari disegnati sul terreno.

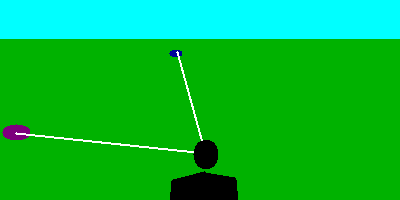
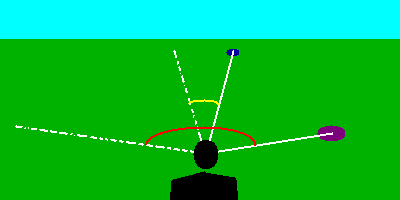
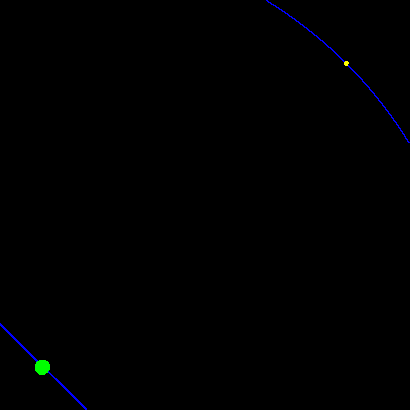
Vedresti quello che la figura ti mostra, cioè che il cerchio più vicino sembra muoversi di più rispetto al cerchio lontano.

Per vederlo meglio, guarda queste 2 figure. Ti mostrano la situazione quando la persona sta a destra delle figure e poi quando sta a sinistra.

Le linee bianche sono le linee di vista dalla persona ai segnali. Nella seconda figura sono lasciate anche le linee di vista della prima figura.

Così puoi vedere che l'angolo compreso tra le linee di vista dirette al segnale più lontano (segnato in giallo) è più piccolo rispetto a quello relativo al segnale più vicino (segnato in rosso).

Per trovare la distanza di oggetti non raggiungibili puoi quindi sfruttare questa relazione tra il tuo spostamento lungo una retta e lo spostamento apparente di un oggetto.

Se due triangoli sono simili, il rapporto tra la base e l'altezza nel primo triangolo è uguale al rapporto tra la base e l'altezza nel secondo triangolo. Avendo misurato i 3 angoli del triangolo grande puoi costruirti un triangolo piccolo, di cui puoi misurare sia la base sia l'altezza. Ad esempio potresti aver trovato che la base del triangolo grande è 6 m, che la base del triangolo piccolo è 12 cm e la sua altezza 30 cm. Allora il rapporto tra base e altezza per il triangolo piccolo è pari a 0,4 e lo stesso vale per il triangolo grande. L'altezza del triangolo grande è quindi 15 m. Questa corrisponde alla distanza tra la retta che hai segnato all'inizio e l'oggetto lontano.

Se il segnale lontano venisse ancor più allontanato l'angolo diventerebbe sempre più piccolo, sinché non riusciresti più ad apprezzare lo spostamento apparente. Questo accade infatti con la Luna. Essa è talmente lontana che la sua posizione apparente sembra fissa anche se ti muovi di parecchi chilometri. L'occhio umano riesce a distinguere solo gli spostamenti angolari più grandi di circa un primo (1'). Quest'angolo corrisponde ad una moneta da 500 lire vista da circa 90m di distanza. Affinché lo spostamento apparente della Luna sia di 1' devi muoverti di circa 112 chilometri!

Per misurare la distanza della Luna con il metodo della parallasse bisogna quindi "segnare" una linea lunghissima e poi mettersi ai due estremi. Allora gli astronomi hanno pensato di usare la rotazione della Terra per procurarsi questa linea.

Immagina di spostarti sull'Equatore. Aspetta che la Luna sorga e segna l'ora. Segna poi di nuovo l'ora quando la Luna è all'altezza massima sull'orizzonte.

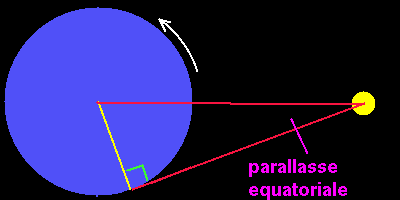
Con questi dati puoi ancora applicare il metodo della parallasse. Infatti il primo angolo è di 90 gradi, il secondo ti viene dato in base alla differenza di orario tra i due istanti, sapendo che la Terra compie un giro di 360⁰ in 23^h 56m 03s. La distanza tra i due punti è uguale al raggio equatoriale terrestre, cioè circa 6378km. Puoi allora trovare la distanza della Luna costruendo ancora un triangolo simile più piccolo e misurabile.

L'angolo indicato dalla scritta nella figura è chiamato parallasse equatoriale orizzontale diurna. Per la Luna esso è pari a 57'2''.44. È un valore medio, in quanto la Luna si muove su un'orbita leggermente schiacciata, quindi la sua distanza dalla Terra varia entro un massimo e un minimo. Con questo angolo e con la misura del raggio equatoriale della Terra si trova che la distanza Terra-Luna è di 384.400km.

Ora sai quant'è lontana la Luna, quindi puoi anche misuare quant'è grande. Non è difficile. Guarda questo esempio. Se conosci la distanza di un tuo amico, puoi determinare la sua altezza confrontandolo con un oggetto vicino a te. Per esempio in questa immagine si usa una moneta da 500 lire. Allontana dagli occhi la moneta finché copre esattamente l'altezza del tuo amico.

Per capire meglio, in questa immagine la situazione è rappresentata con uno schema. Come vedi, congiungendo i tuoi occhi con la moneta e con la persona si formano due triangoli simili.

Allora il rapporto tra le basi dei due triangoli è uguale al rapporto delle loro altezze. Nel caso della nostra figura, il rapporto tra le dimensioni della moneta e quelle del tuo amico è uguale al rapporto delle loro distanze da te.

Supponiamo ad esempio che tu ti sia allontanato di 20m, cioè 2000cm, dal tuo amico. La moneta da 500L copre il tuo amico quando la metti a 30cm dagli occhi. Allora il rapporto tra l'altezza del tuo amico e quella della moneta è uguale a 2000/30. Lo stesso rapporto esiste tra il diametro della moneta e l'altezza del tuo amico. Visto che una moneta da 500L ha un diametro di circa 2,6cm, il tuo amico è alto circa 173,3cm.

La stessa moneta copre la Luna quando la tieni a 287,6cm. Il rapporto tra distanza della Luna e distanza della moneta è quindi circa 133657858. Questo rapporto moltiplicato per 2,6cm ti dà allora circa 3475km (fai tu la conversione delle unità di misura!).

La Terra è quindi 3,7 volte più grande della Luna, e la distanza Terra-Luna è uguale a circa 30 volte le dimensioni della Terra.

Questa immagine ti mostra il sistema Terra-Luna con i due corpi e la distanza tra di loro sulla stessa scala. La Terra è colorata in verde, la Luna in giallo. Le curve blu sono le tracce delle orbite della Terra attorno al Sole e della Luna attorno alla Terra.

Anche questa immagine ti mostra come lo spazio interstellare è in gran parte vuoto. Tra la Terra e la Luna c'è una distanza molto maggiore delle loro dimensioni. Se ad esempio volessi andarci in macchina, a 100 km/h impiegheresti più di 5 mesi (un po' più di 160 giorni).

Quanto impiega la Luna a compiere un giro attorno alla Terra? Il periodo può essere trovato cronometrando quanto impiega la Luna a passare due volte per lo stesso punto del cielo. Per esempio puoi segnare il momento in cui copre una certa stella, e aspettare sino a quando ha compiuto un giro attorno alla Terra e la copre di nuovo. Troveresti allora circa 27 giorni (27 giorni, 7 ore, 42 minuti).

Quanta massa è contenuta nella Luna? Per saperlo puoi sfruttare l'attrazione reciproca di Terra e Luna. Sotto l'effetto della forza di gravità i corpi si muovono seguendo le tre leggi di Keplero. In seguito imparerai a conoscere queste leggi, che regolano il moto di un corpo attorno ad un altro.

Quando hai due corpi di massa confrontabile che orbitano l'uno attorno all'altro la terza legge di Keplero stabilisce un legame tra il periodo orbitale dei due corpi, la loro distanza media e le loro masse. Questa legge vale anche nel caso del sistema Terra-Luna. Usando questa legge puoi quindi trovare la massa della Luna se conosci la massa della Terra, il periodo orbitale della Luna e la distanza media Terra-Luna.

Questi dati li conosci già e con la terza legge di Keplero si trova che la Luna ha una massa che è 0,012 volte quella della Terra (cioè circa un centesimo). Avendo la massa e il raggio della Luna, puoi ora trovare quant'è la forza di gravità sulla superficie del nostro satellite naturale.

La forza è proporzionale alla massa, quindi se sotto i tuoi piedi la Luna venisse messa al posto della Terra noteresti una forza di gravità pari a circa un centesimo di quella della Terra. Ma la Luna è più piccola della Terra, quindi puoi avvicinarti di più al suo centro. In tal caso sai che la forza aumenta con l'inverso del quadrato della distanza. Il rapporto tra le dimensioni dei due corpi è circa 3,7, quindi il rapporto tra le forze di gravità è circa 13,7 (3,7²). Il prodotto tra 0,012 e 13,7 fa circa 1/6. Il tuo peso sulla Luna sarebbe quindi 1/6 rispetto a quello che hai sulla Terra.

Di che cosa è fatta la Luna? Comincia a guardare come si presenta la sua superficie. Ciò che si vede guardando la Luna è mostrato molto bene in questa foto. Ci sono aree chiare ed aree scure. Le aree scure vengono chiamate mari, ma non contengono acqua. I mari sono regioni pianeggianti, mentre le aree chiare sono corrugate e sono in media più elevate. Per questo vengono anche chiamate altopiani.

Su tutta la superficie sono evidenti i crateri causati dall'impatto di meteoriti. I crateri sono molto più appariscenti e frequenti nelle zone chiare. Negli anni dal 1969 al 1972 la Luna è stata esplorata dall'uomo. Più in basso puoi vedere il veicolo lunare della missione Apollo 15 vicino al monte Hadley. Gli astronauti hanno riportato sulla Terra campioni di suolo lunare, quindi è stato possibile analizzare e datare le rocce.

Si è scoperto che le rocce lunari più giovani sono quelle scure dei mari ed hanno 3,2 miliardi di anni. Le più vecchie sono quelle chiare degli altopiani ed hanno 4,6 miliardi di anni.

Pur avendo una massa pari ad un centesimo di quella della Terra, il rapporto tra la massa della Luna e quella della Terra è molto alto, se confrontato con quello che avviene per gli altri pianeti. Se si esclude il sistema Plutone-Caronte, il sistema Terra-Luna è in effetti un caso unico nel Sistema Solare. In genere i satelliti sono molto più piccoli rispetto ai pianeti che li trattengono in orbita. Legato a questa particolarità c'è un fenomeno che conosci bene. Le maree. Se vuoi saperne di più puoi cliccare qui.

Guarda questo filmato sulla Luna e la sua esplorazione da parte dell'uomo.

La missione Apollo 11

(NASA/JPL), AVI , 5.8 Mb